运筹学M法求解详细过程案例
1、题目:max z = 2*x1 - x2 + 2*x3;s.t. [ x1 + x2 + x3 >稆糨孝汶;= 6 ; -2*x1 + x3 >= 2 ; 2*x2 - x3 >= 0 ; xj >= 0 ]
2、首先将给出的线性规划问题化为标准型,这样才有利于后面的引入人工变量M。

3、在化为标准型的基础上我们引入人工变量M。
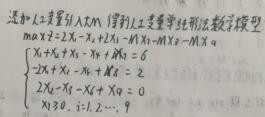
4、根据引入M后的目标函数和约数方程构建单纯形表进行迭代计算。这里求的是“max”所以我尺攵跋赈们要将最后一行所有数值都迭代成负值。

5、经过上式的迭代之后,我们发现结果仍然不满足条件,那么我们就需要将原式继续迭代,寻找进基变量和出基变量。

6、根据最大值,在上式的迭代结果中,我们选择“5+4M”为进基变量,再由后边的比值确定“4”为出基变量。
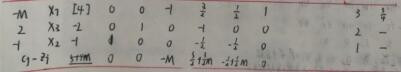
7、经过这几轮迭代之后,我们得到下式,但是下式虽然仍然存在正值,但是那一列对应的数值都小于0 ,那么我们就没有办法确定出基变量,所以结束迭代计算。
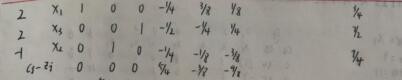
8、根绝定义我们得出:原线性规划问题无最优解。
