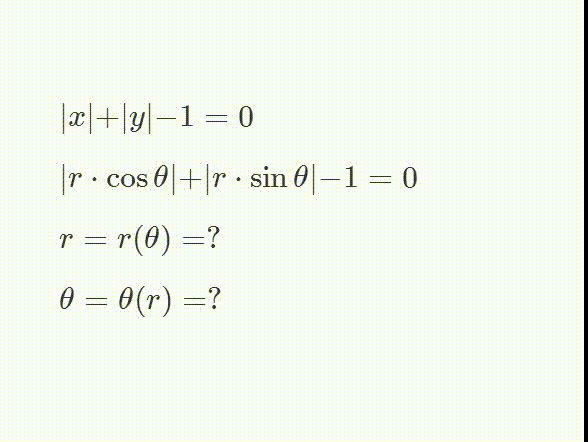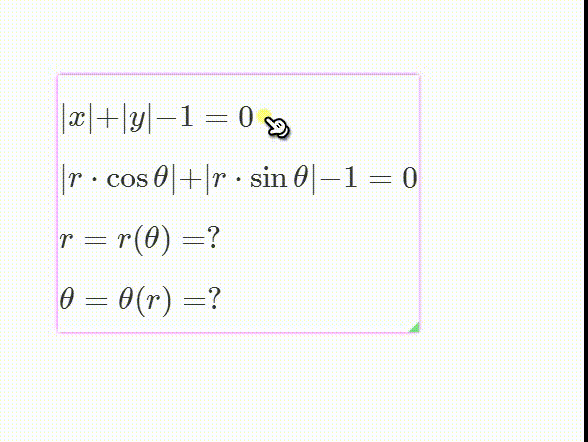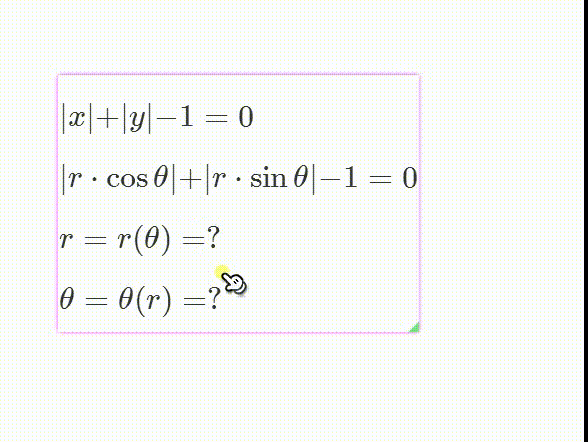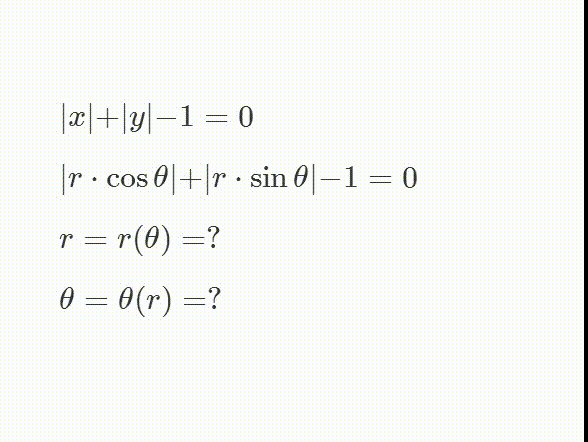极坐标方程下极角和极径颠倒一下会怎样

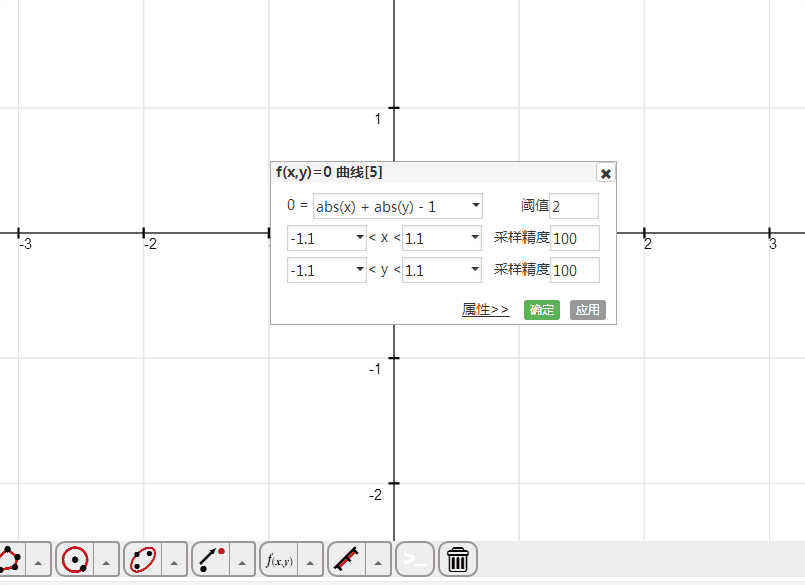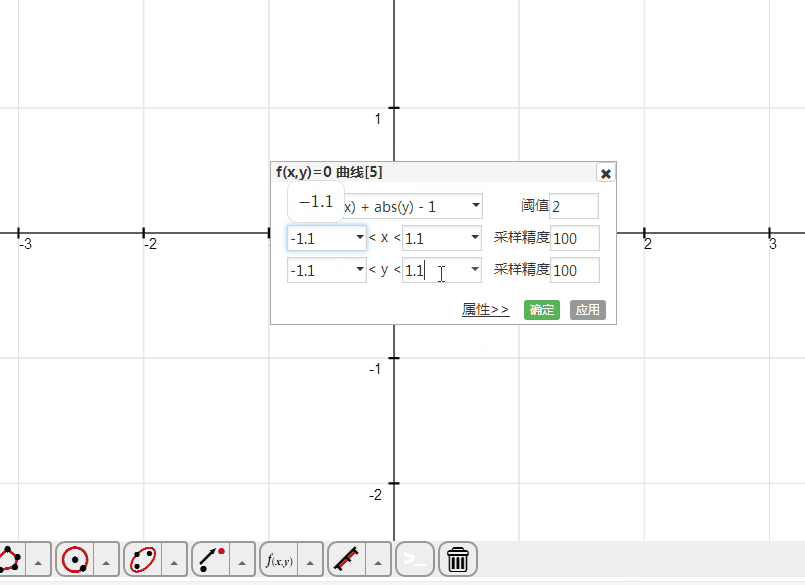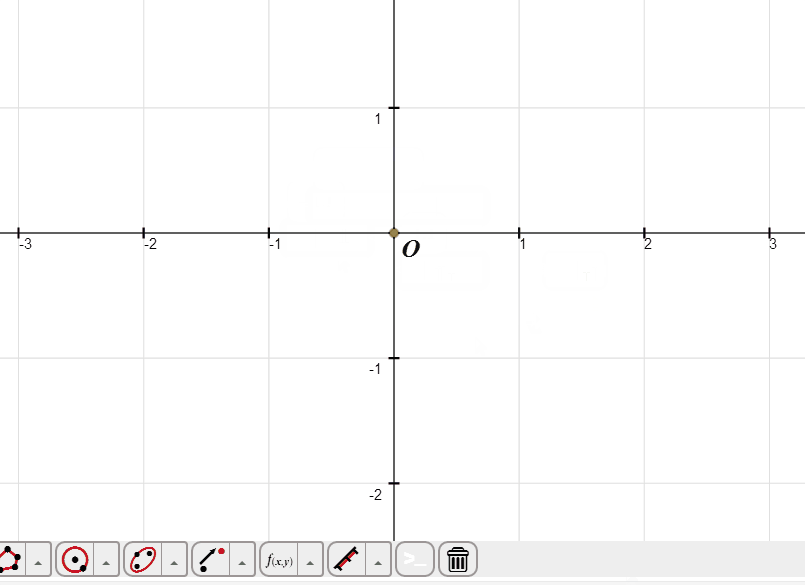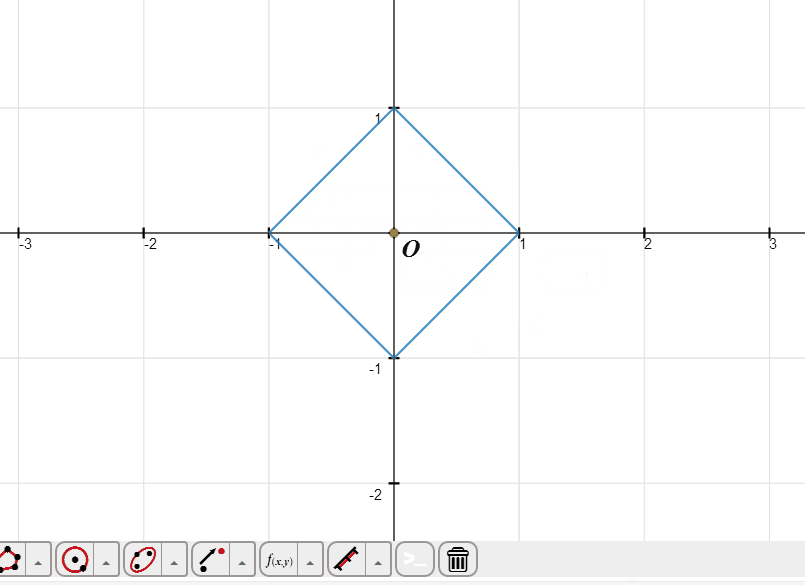
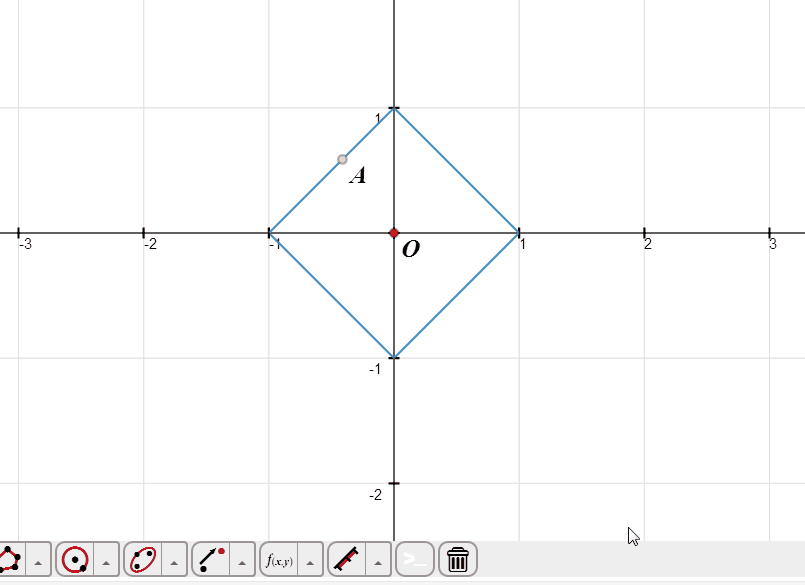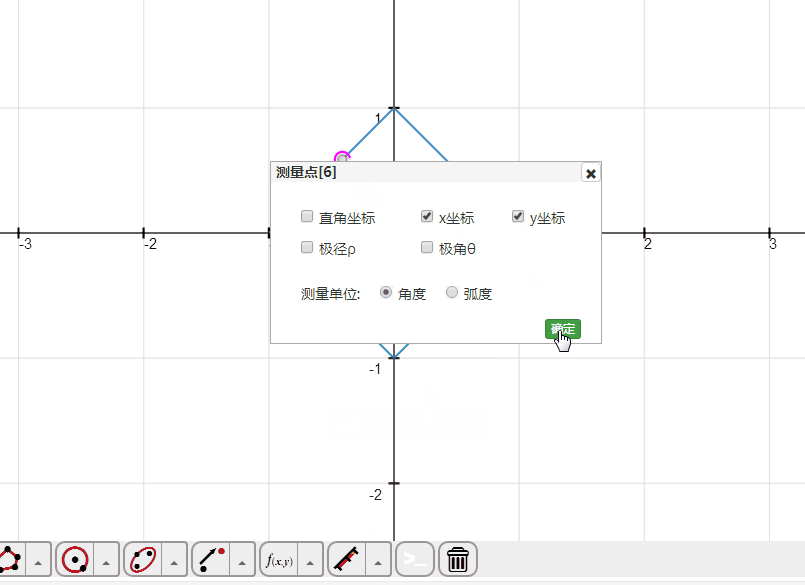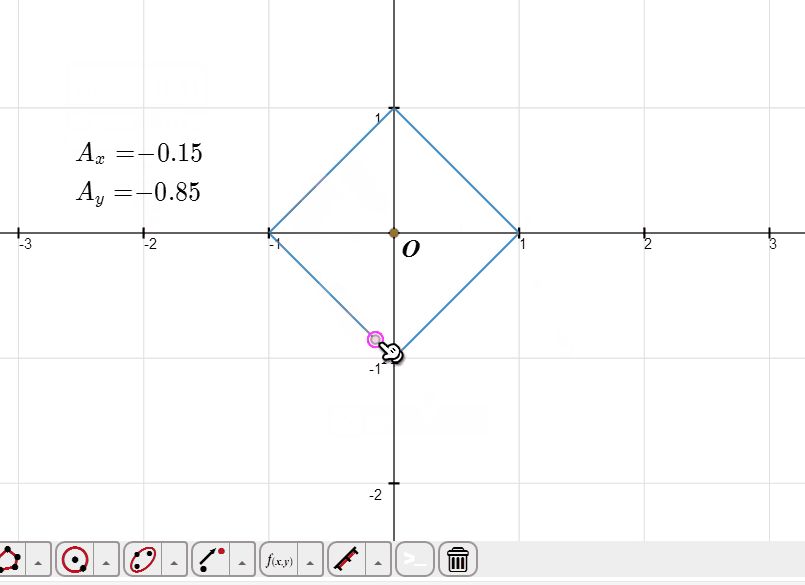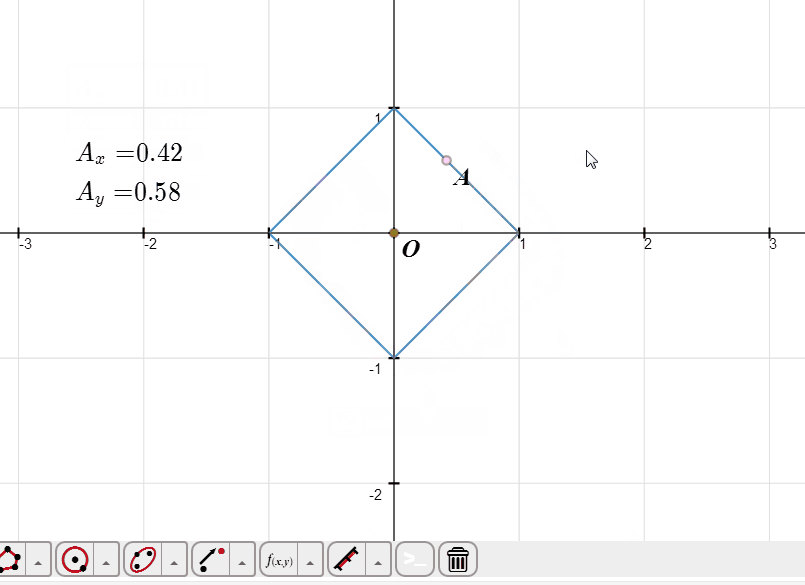
1、绘制隐函数方程——abs(x) + abs(y) - 1=0的图像。

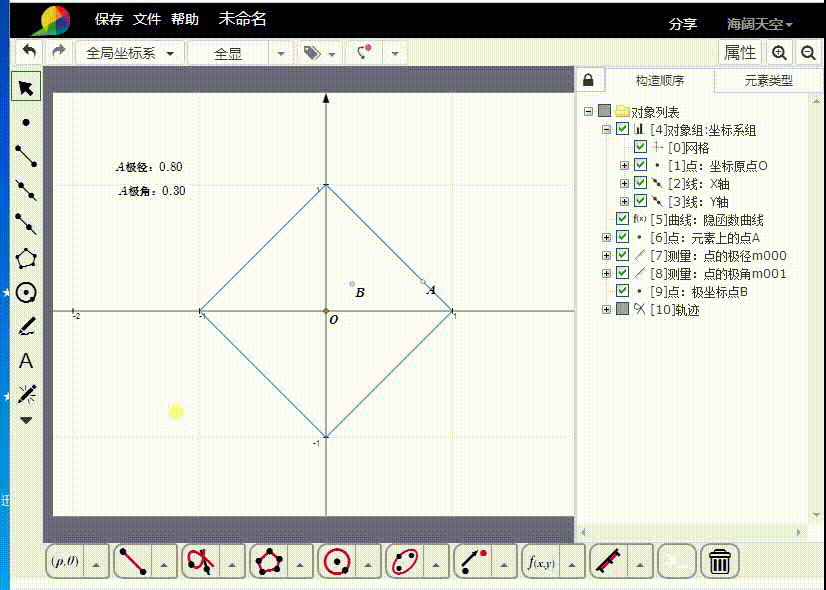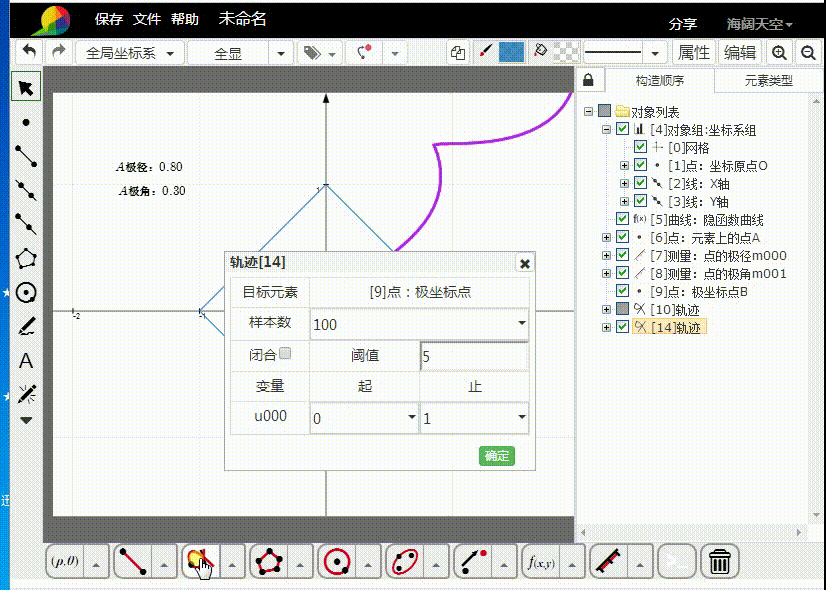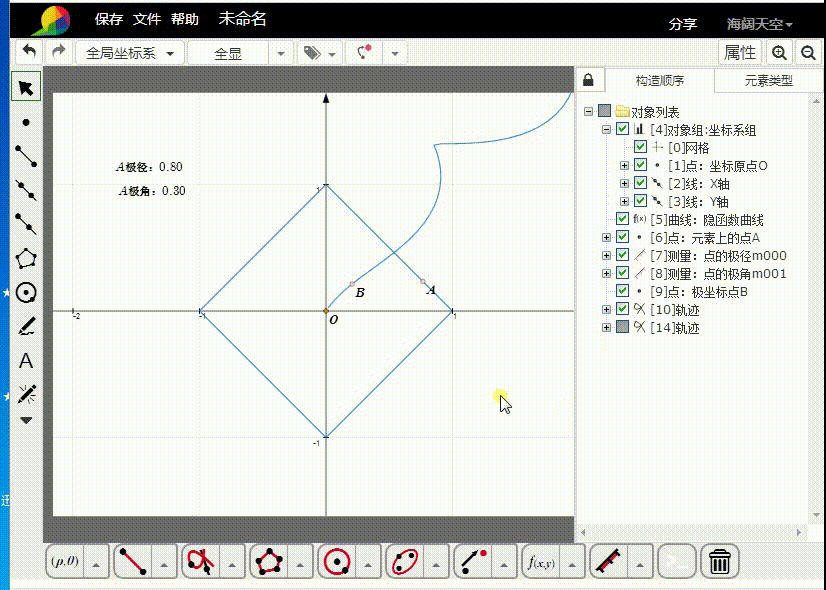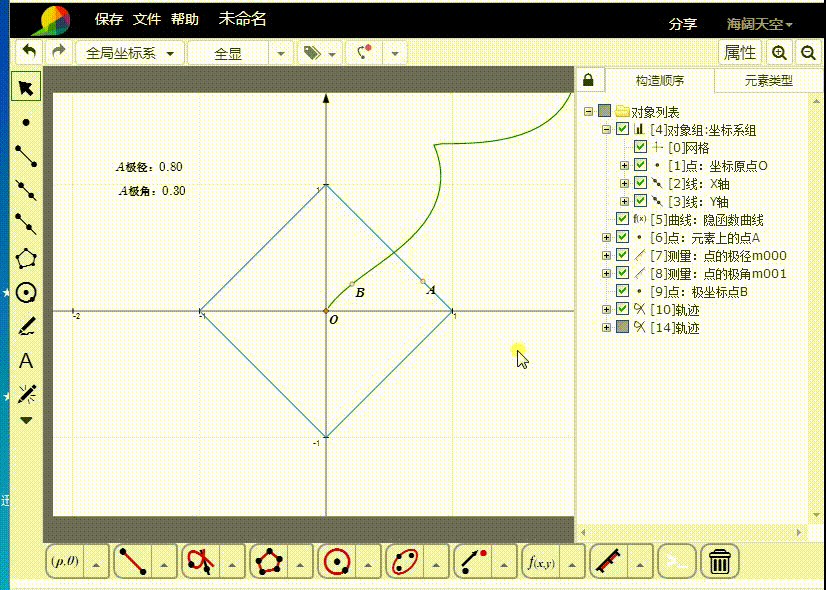
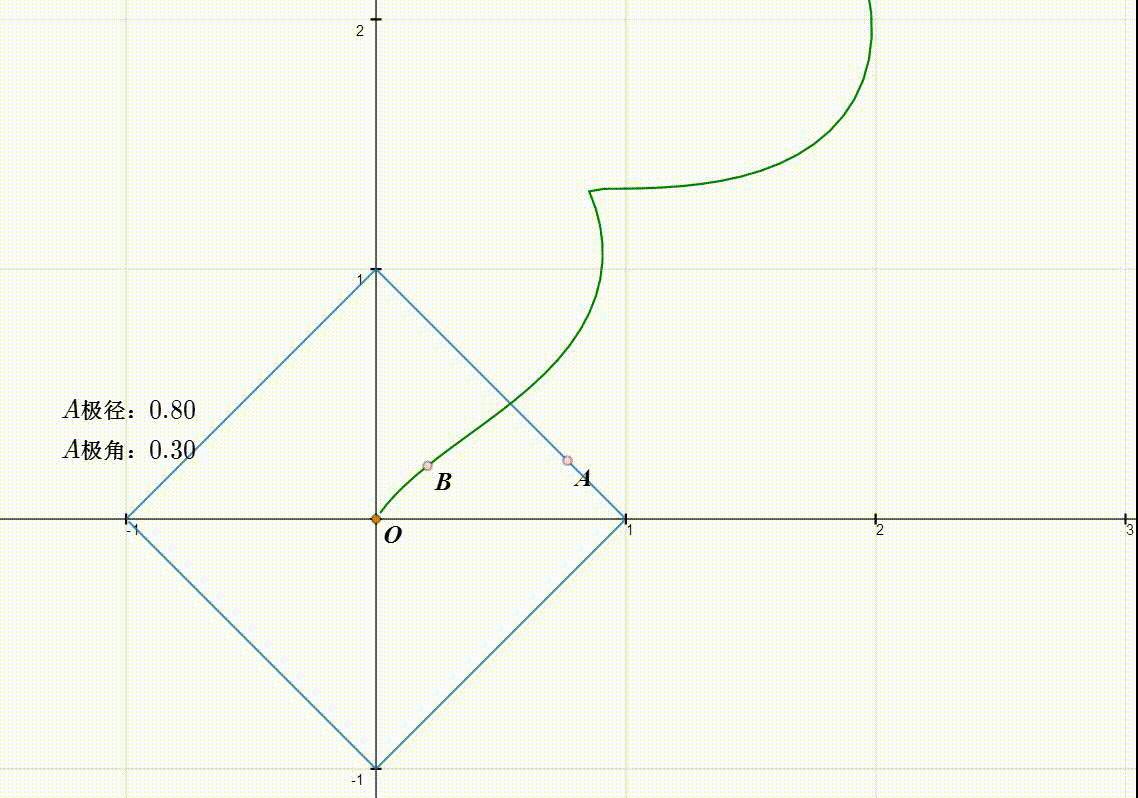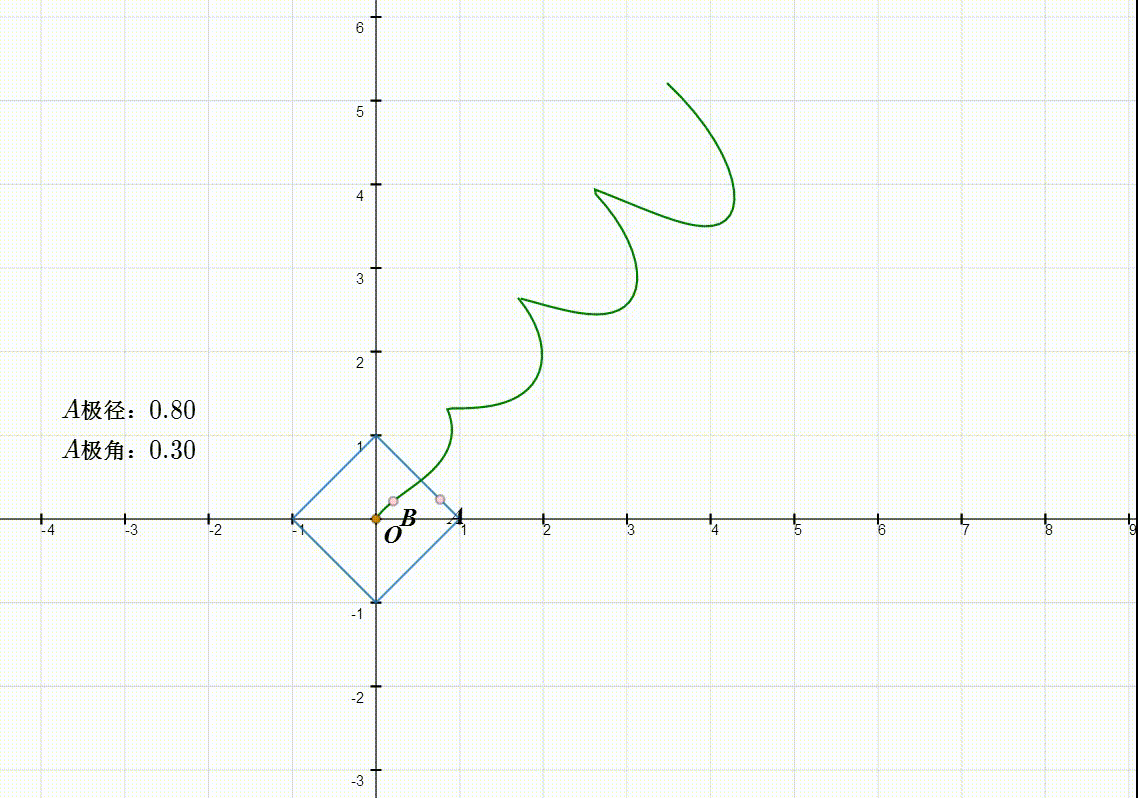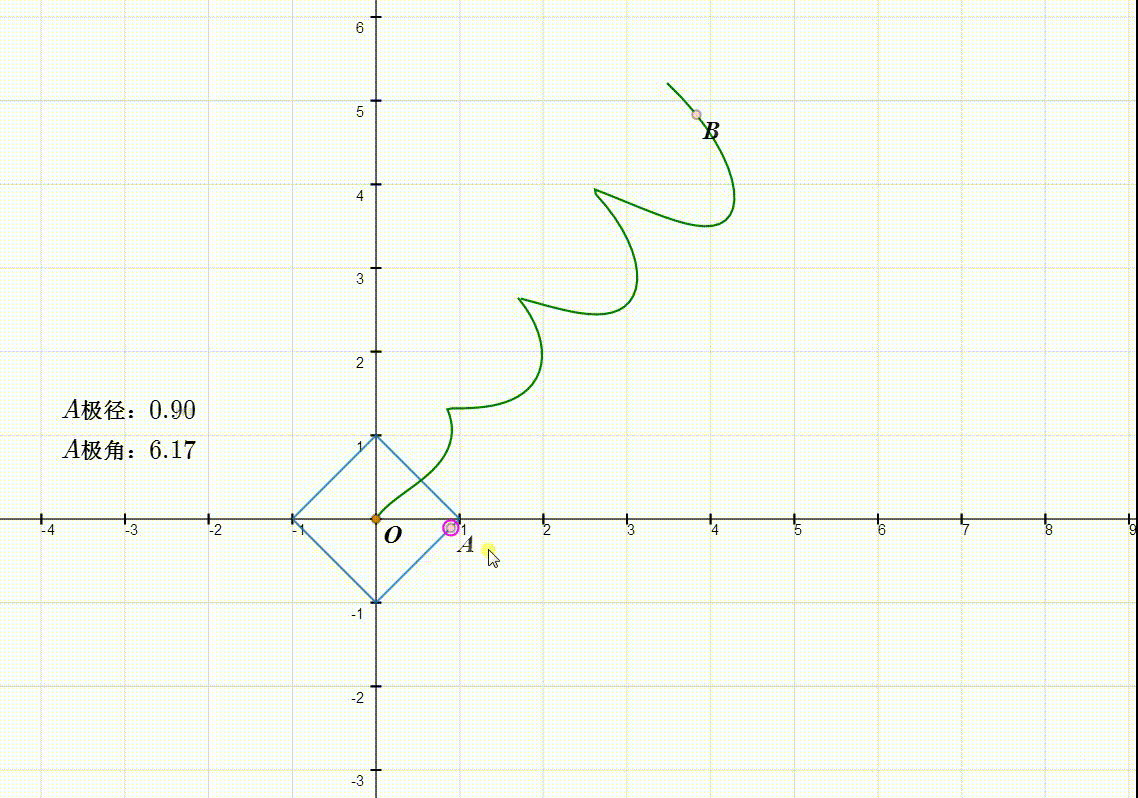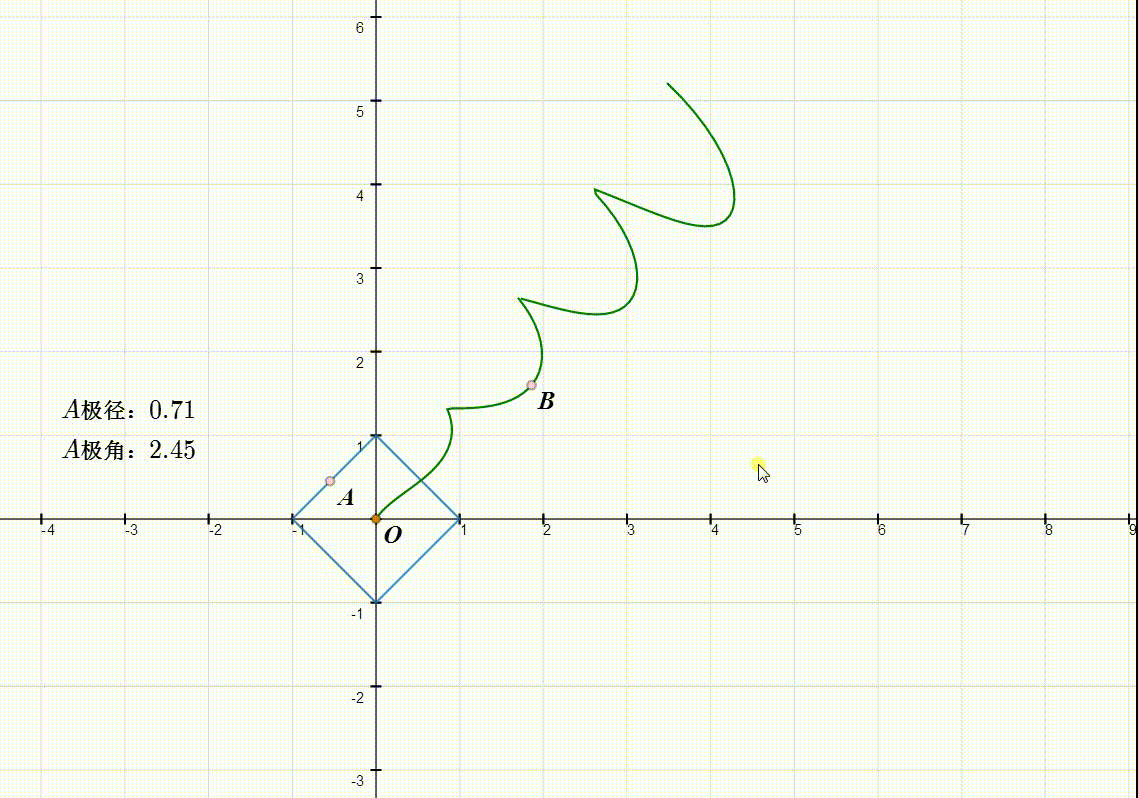
2、设A是图像上的动点，测量A的极角和极径。

3、绘制极坐标点B，其中，B的极径是A的极角，而A的极径则是B的极角。

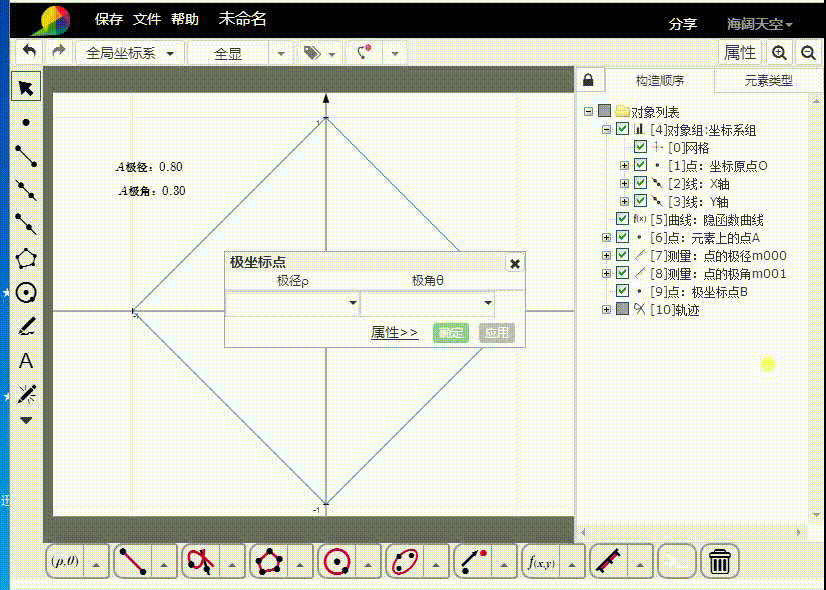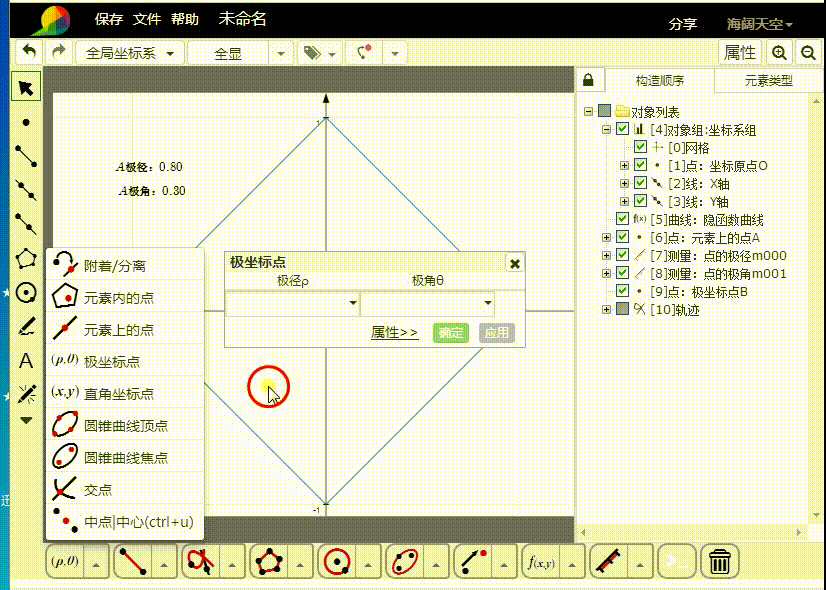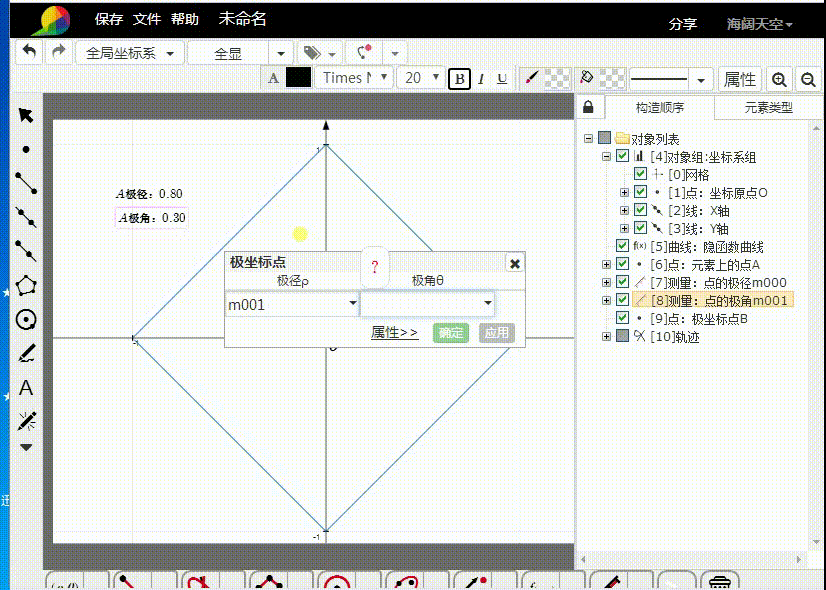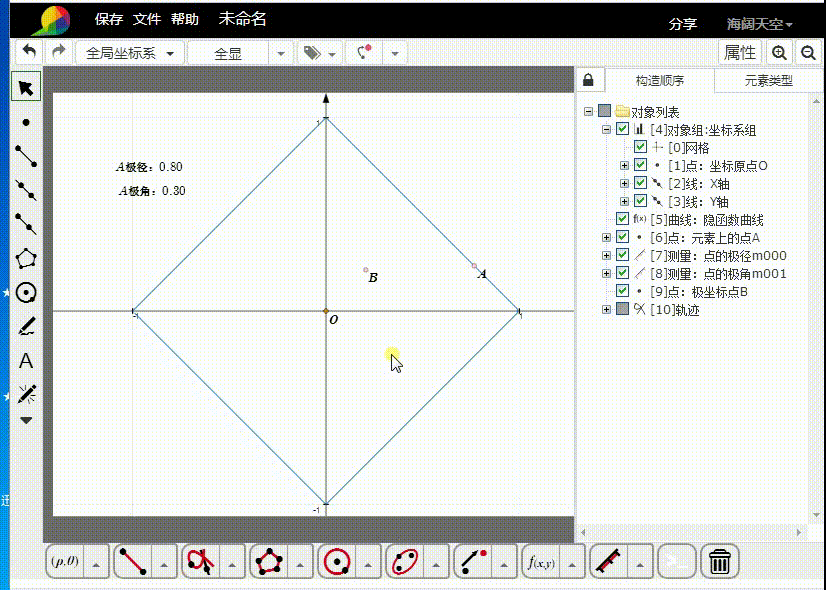
4、根据A来构造B的轨迹。

5、缩小坐标系，可以看到B的轨迹的完整图形。

6、如果把abs(x) + abs(y) 颍骈城茇- 1=0写成极坐标的形式的话，就是：abs(r*cos(θ)) + abs(r*sin(θ)) - 1=0这很难把θ和r分离开来，但是，我们却可以画出对应的极坐标图像。本文在上面的过程，就是这类问题的解法。